Research

Nonequilibrium mixtures and active droplets

Our research investigates the physics of active soft matter systems and biomolecular condensates, with a strong focus on understanding diffusion and transport phenomena in complex, nonequilibrium environments.

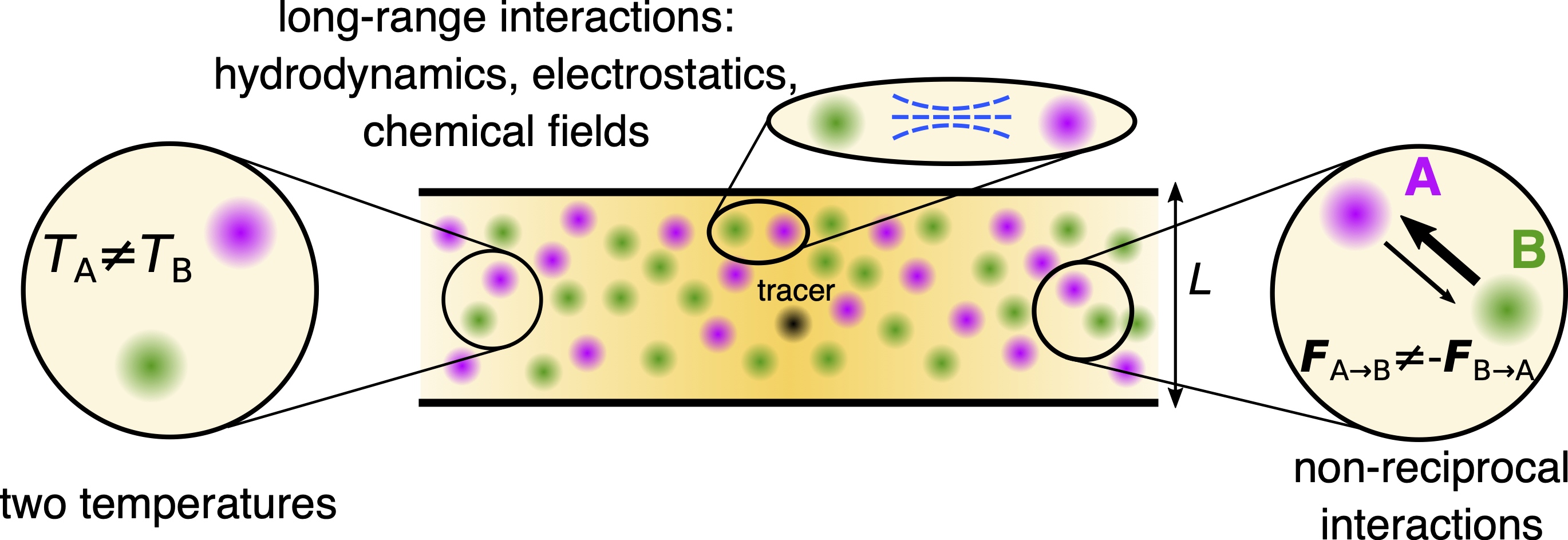
A significant part of my work explores the diffusion of tracer particles within dense mixtures of soft particles, connected to different thermostats or with non-reciprocal interactions, revealing how activity and crowding affect tracer mobility and challenge classical diffusion theories. I develop analytical frameworks based on linearized density field theories and path-integral methods that accurately describe tracer diffusion in these heterogeneous and active media.

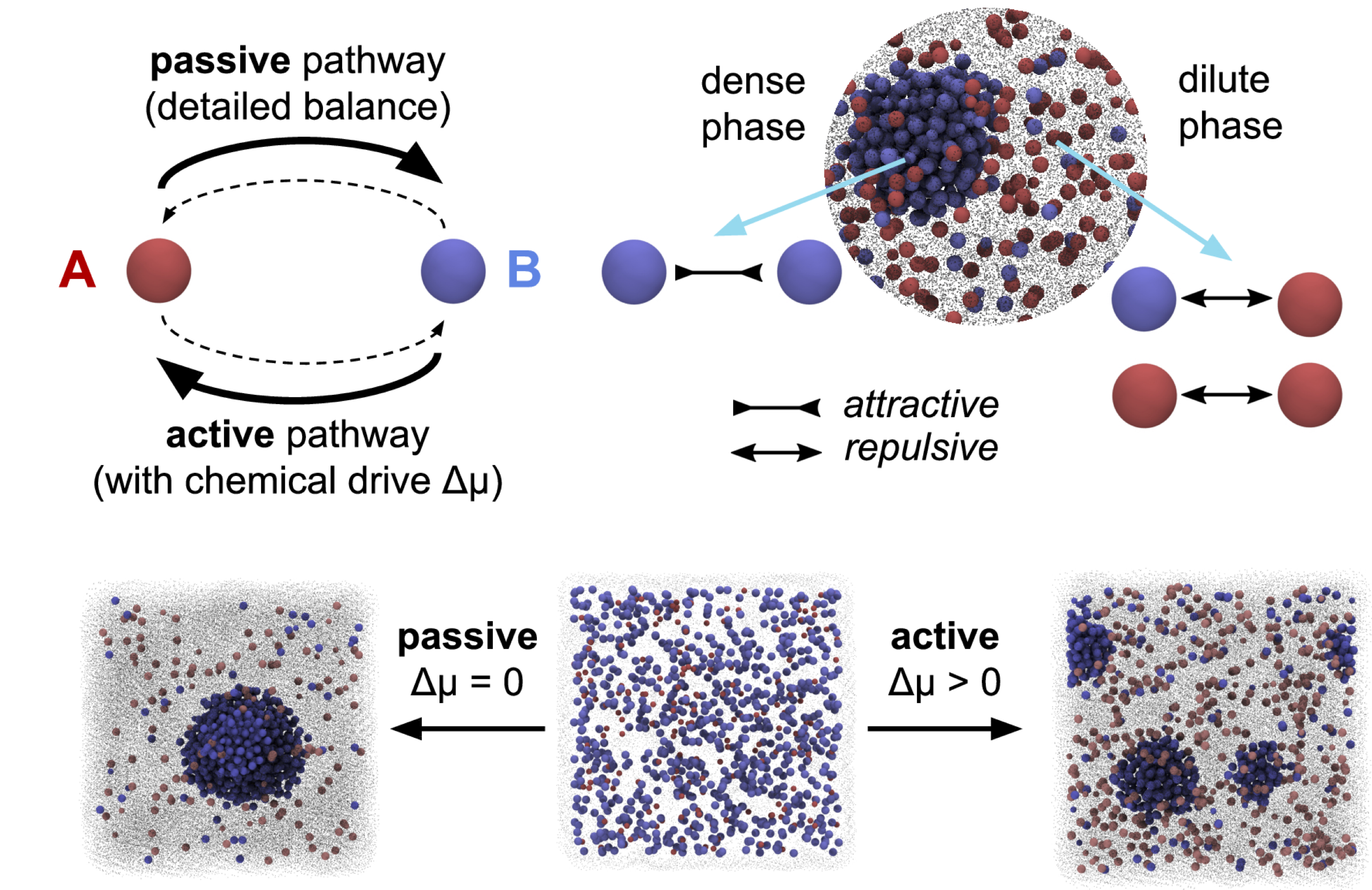
Additionally, using a combination of microscopic stochastic simulations and analytical approaches, we study how enzymatic reactions and molecular interactions govern the formation, stability, and dynamics of chemically active droplets and biomolecular condensates, which play crucial roles in cellular organization. Additionally, I investigate how chemically active droplets modulate molecular encounter kinetics, showing that condensates can both accelerate and hinder biochemical reactions depending on the interplay of reaction-driven fluxes and transport limitations. These findings deepen our understanding of transport processes in biologically relevant crowded and active environments, connecting microscopic interactions to emergent nonequilibrium behaviors.

Charged, Coulomb-like and polar suspensions

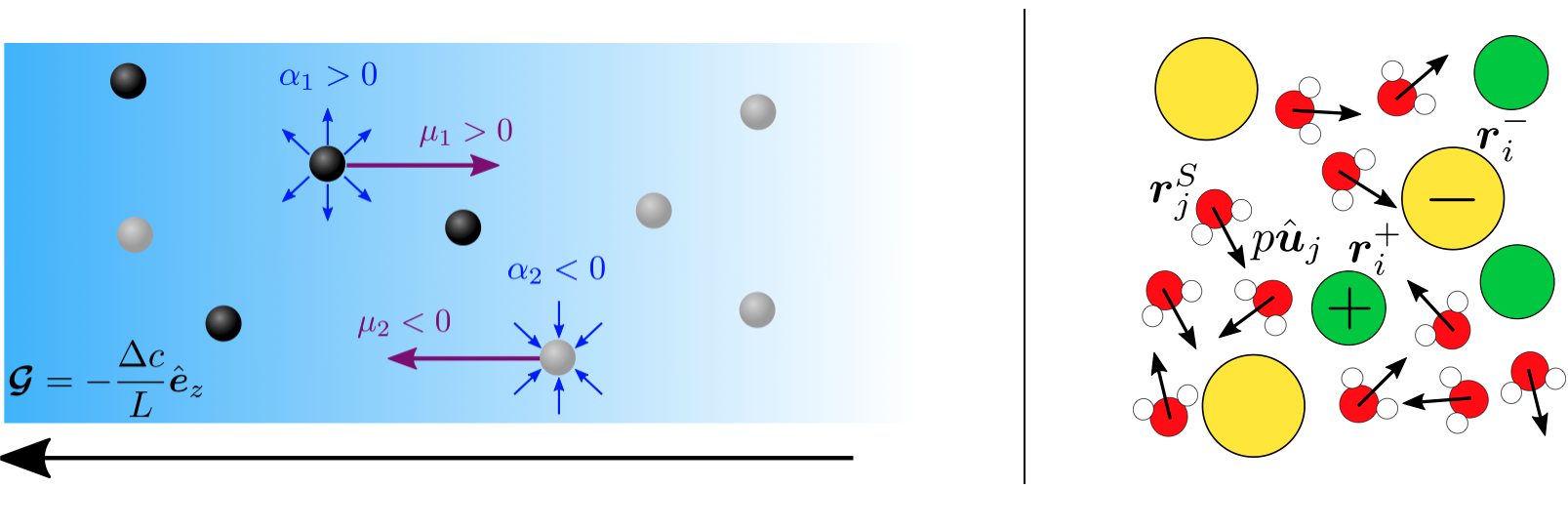
We also aim at advancing our understanding of transport phenomena in electrolytes and chemically active systems by developing theoretical models that incorporate microscopic fluctuations and solvent effects. We have extended stochastic density functional theory (SDFT) to explicitly account for the polar nature of solvents, enabling the computation of key observables such as charge structure factors and dielectric susceptibilities. This approach highlights how ion–solvent interactions influence the dynamic behavior of electrolytes. In parallel, I have analyzed transport properties in concentrated electrolytes, such as conductivity and self-diffusion, evaluating recent approximations within SDFT and comparing them with classical theories. This work emphasizes the importance of short-range interactions and hydrodynamic corrections in improving theoretical predictions.

Additionally, I have explored analogies between chemotactic particles and strong electrolytes, showing how nonreciprocal interactions lead to effective mobility laws that extend Debye-Hückel-type theories to nonequilibrium systems. These results contribute to bridging electrolyte theory and active matter, with potential applications to nanoscale transport in complex environments.

Stochastic dynamics of interacting particles and tracer diffusion

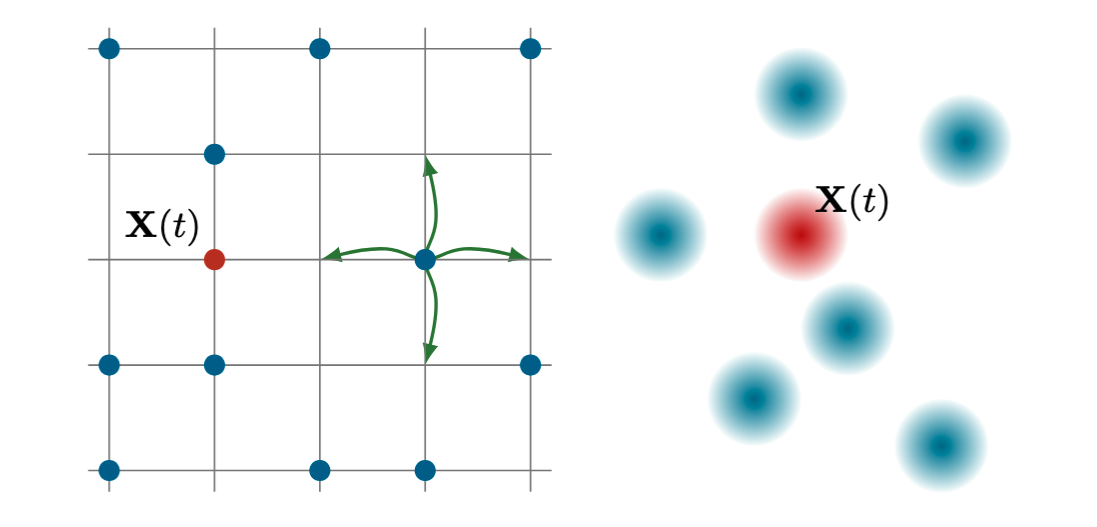
We have developed theoretical tools to describe fluctuation phenomena in systems of interacting particles, with a focus on stochastic density functional theory and the Dean-Kawasaki equation. I derived exact non-Gaussian correlations beyond standard linearized treatments of the Dean-Kawasaki equation and reviewed its foundational role in stochastic density functional theory, highlighting connections with frameworks such as fluctuating hydrodynamics and macroscopic fluctuation theory.

We also investigated the dynamics of interacting Brownian particles in confined geometries and revealed universal correlation profiles in single-file transport. In other studies, we proposed a microscopic theory for absolute negative mobility in crowded active systems and extended linear response theory for driven tracers in the symmetric exclusion process. We further derived an exact closure for spatial correlations in single-file diffusion, providing new insights into the structure of interactions that give rise to anomalous transport.